Problem:

Let ABCD be a quadrilateral. Let E be the midpoint of AB, F the midpoint of BC, G the midpoint of CD, and H the midpoint of DA. Prove that EFGH is a parallelogram.

Show Solution

Solution:

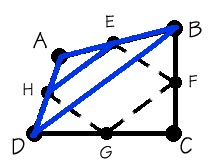Draw Diagonal DB. Then HE is a midline of ADB, so HE:DB = 1:2, and HE||DB. Also, GF is a midline of CBD, so GF:DB=1:2, and GF||DB. Through transitivity, GF||HE, and GF=HE. Applying the same argument to the opposite pair of sides, we can see that EFGH is a parallelogram. A representation of one of the triangles and its midline can be seen on the left.